Sobolev imbedding and interpolation inequalities.

索伯这块内容确实又繁琐又多, 所以这里妄图梳理一个快速查询的笔记.

一些重要的不等式

Holder

Young

Minkowski

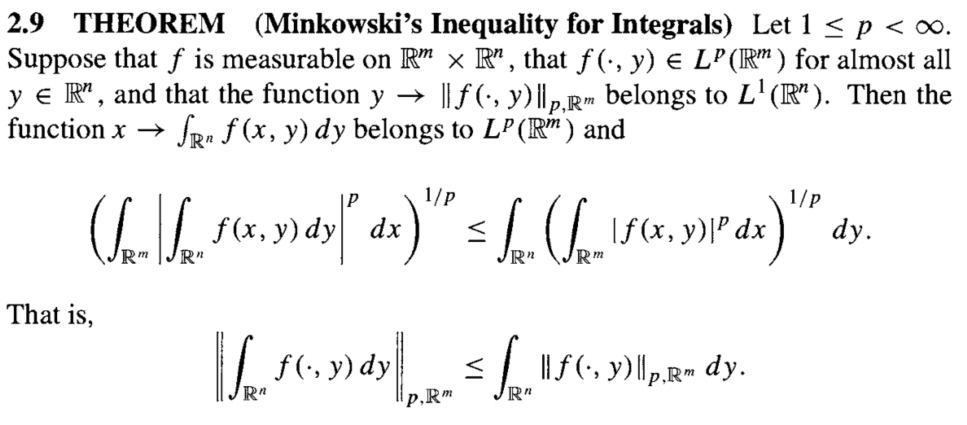
Marcinkiewicz插值定理

这是一个非常强大的插值定理, 允许我们通过弱型不等式来得到强型不等式. 这里放出定理的陈述和证明. 便于后续使用.

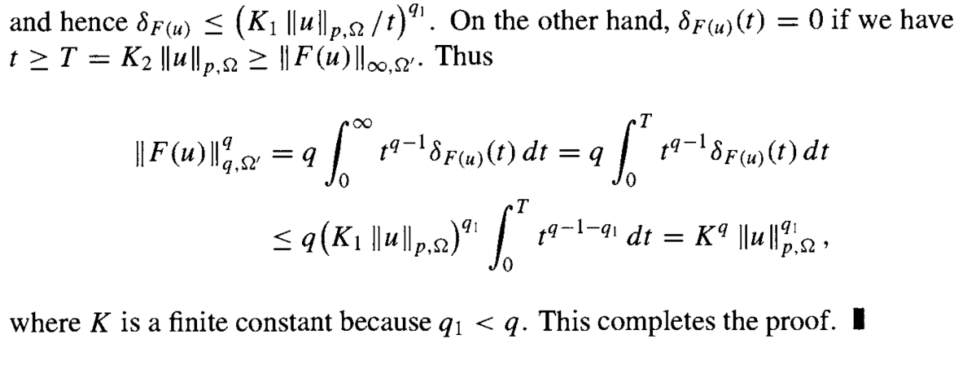
geometry of domain

这里主要放一些区域的几何条件, 便于后续使用.

segment condition

$\forall x \in \partial \Omega, \exists$ 一个向量 $y_x$, 使得对于 $\forall z \in \overline{\Omega} \cap B(x, r_x), \forall t \in (0,1)$, 有 $z + t y_x \in \Omega$.

就是说, 对于边界上的每个点, 都存在一个方向, 使得它附近的点沿着这个方向移动一小段距离后形成的的线段都在区域内.

由于$\partial \Omega$有局部有限的可列覆盖, 所以可以取一列局部有限的开集 ${U_i}$ 覆盖 $\partial \Omega$, 然后每个$U_i$对应一个向量 $y_i$.

weak cone condition

弱锥条件是说, 对于区域中的每个点, 它出发的射线与单位球的交集测度一致大于某个正数 $\delta > 0$.

cone condition

锥条件是说, 对于区域中的每个点, 都存在一个锥, 它的顶点在该点, 并且整个锥都包含在区域内. 这个锥必须同构于某个固定的$(\rho, \kappa)$锥.

uniform cone condition

一致锥条件有些类似于segment condition. 从一列局部有限的开集 ${U_i}$ 覆盖 $\partial \Omega$, 然后每个$U_i$对应一个锥 $C_i$, 这些锥的参数 $(\rho, \kappa)$ 是相同的, 它们满足以下条件

• $U$_j$ 的半径有上界
• $U_j$ 的并包含 $\partial \Omega$ 的某个 $\delta>0$ 邻域
• 对于 $\forall x \in \partial \Omega \cap U_j$, 有 $x + C_j \subset \Omega$.
• 任何超过R个 $U_j$ 都没有交集.

容易看出, 一致锥条件蕴含锥条件, 锥条件蕴含弱锥条件.

strong local lipschitz condition

强局部Lipschitz条件是说, 对于区域中的每个边界点, 都存在一个局部坐标系, 使得在该坐标系下, 区域的边界可以表示为某个Lipschitz函数的图像. 具体的, 同样选局部有限开覆盖 ${U_i}$, 对于每个$U_i$ 对应一个M-Lipschitz函数, 使得

• 超过R个 $U_j$ 都没有交集.

• 如果两个点 $x,y \in \Omega_\delta$ 且 $

  x-y

  < \delta$, 则它们属于同一个 $U_j$.

• $\Omega \cap U_j$ 是对应的Lipschitz函数的上方区域.

uniform $C^m$ condition

选局部有限开覆盖 ${U_i}$, 对于每个$U_i$ 对应一个 $C^m$ 函数 $\Phi_i$ 是从 $U_i$ 到单位球的坐标映射, 使得

• 超过R个 $U_j$ 都没有交集.
• 1/2单位球覆盖 $\partial \Omega$ 的某个 $\delta>0$ 邻域.
• $\Phi_i(\Omega \cap U_i)$ 是单位球的上方区域.
• 所有阶数小于等于m的导数都一致有界.

Sobolev imbedding

首先, 空间的嵌入定理, 主要按照函数空间的奇性来划分. 由于是积分范数, 所以n维空间的积分可以提供$x^{n/p}$, 而求导数会损失$x^m$的奇性, 所以对于 $m,p$ 的Sobolev空间$W^{m,p}$, 其容纳的奇性大概为 $x^{n/p - m}$. 所以分类的临界值为 $mp = n$. $mp>n$ 时, 函数比较光滑, 可以嵌入到连续函数空间中; $mp<n$ 时只能嵌入普通的$L_q$空间. 具体不等式如下:

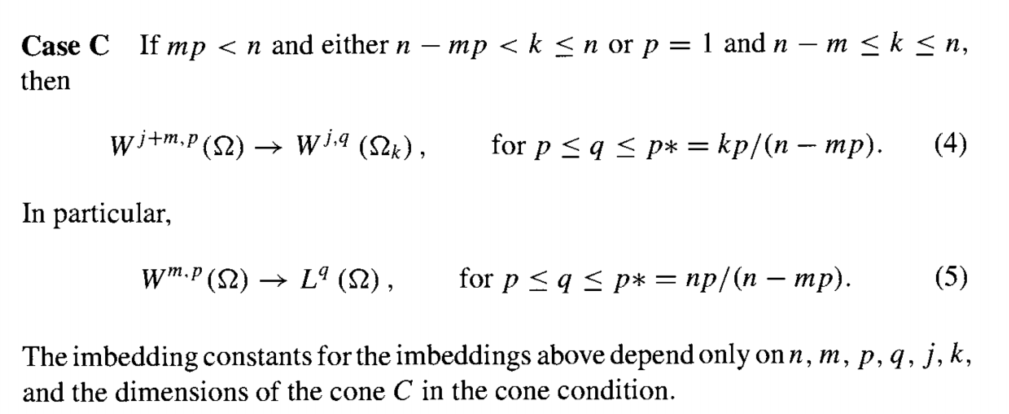
除了部分边界情况以及需要区域有lipshitz条件的第二个part, 其余证明利用了区域的cone condition, 然后使用cone上的积分平均值来控制函数值. 积分平均值来自于potential估计.

核心的不等式为

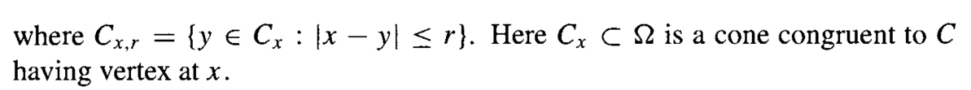
这个不等式来源为带积分余项的泰勒展开, 将函数值用导数展开后在cone上积分. 最终得到的结果类似于

对于$mp>n$, $p>1$的情况

而$p=1$, $m=n$, $\omega_m = 1$, 不等式恰好是自然成立的.

对于k维超曲面的trace估计, 则是直接将上面的不等式的p次方在超曲面上积分即可, 然后用Holder的插值不等式进行估计即可.

利用插值不等式, $p\le q \le p^* = \frac{kp}{n-mp}$, 则有 \(\|u\|_{q, H} \le \|u\|_{p^*, H}^\theta \|u\|_{p, H}^{1-\theta} \\ \le K (\sum_{|\alpha|\le m} \|\chi_1 \omega_m * |D^\alpha u| (x)\|_{p^*,H})^{\theta} \\(\sum_{|\alpha|\le m} \|\chi_1 \omega_m * |D^\alpha u| (x)\|_{p,H})^{1-\theta}.\)

也就是只需要证明$q=p$和$q=p^*$的边界情况. 核心的估计为对于$v \in L^p$, 有

这两个不等式中的系数可以直接算出来. 第一个中, 左侧贡献 $m-k/p$, 右侧贡献 $n/p$, 所以出现一个 $m - \frac{n-k}{p}$.

第二个中, 左侧贡献 $m - \frac{k}{p^*} = \frac{n}{p}$

它们分别是直接进行估计和使用 Marcinkiewicz插值定理得到的. 这个插值定理非常强大的地方在于, 它允许我们只需要证明两个端点的弱型不等式, 就可以得到开区间的强型不等式. 如果弱不等式在某个区间上成立, 那么中间的强不等式也成立.

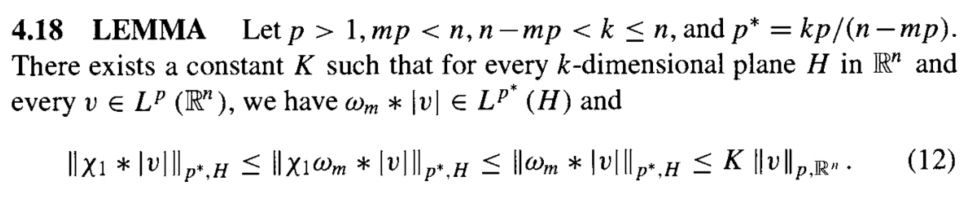
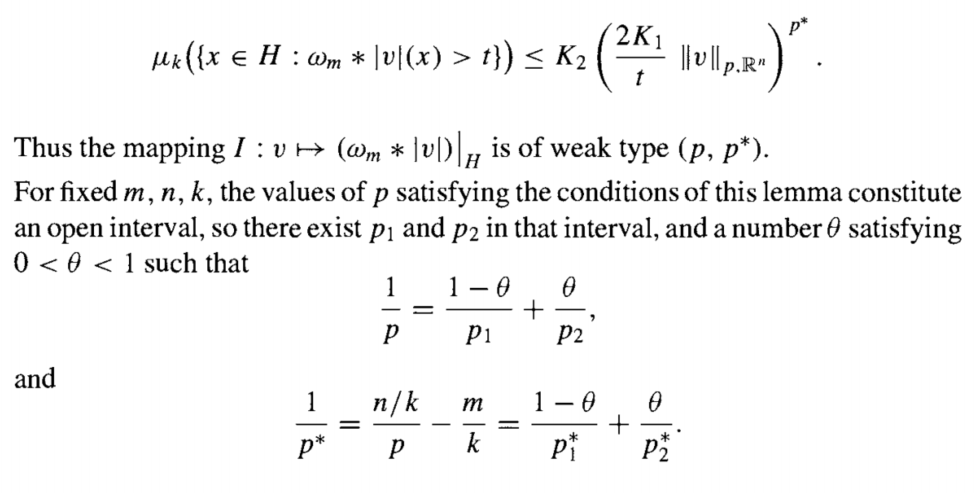
$mp=n, p>1$的情况, 同样的考虑插值. 我们希望证明 $p\le q < \infty$ 的情况.

选择 $1 < p_1 < p < p_2$, 由于 $n-mp_1 < k$, 因此有

同时 $mp_2 > n$, 因此有

因此如果

要证明的不等式就会成立. 而只要$p\le q < \infty$, 就总能找到合适的$p_1, p_2$使得上面的等式成立. 而$q=\infty$的情况则不成立. $p=q$的情况对应于$p_2 = \infty$, 对应也成立.

只剩下$p=1, mp<n$, 此时可以直接进行证明, 它的证明思路与索伯列夫不等式类似, 通过向量值holder不等式进行估计.

$p=1, n-mp < k \le n$, 则要证明 $W^{m,1} \to L^{\frac{k}{n-m}}(H)$. 但是 $W^{m,1} \to W^{m-1, p}$, $1\le p \le \frac{n}{n-1}$.

但是此时有 $k \ge n-m+1 > n - (m-1)p$, if $p>1$. 因此可以使用之前的结论, 有它可以嵌入 $L^{q}(H)$, $1 \le q \le \frac{kp}{n-(m-1)p} = \frac{k}{n-m}$.

最后的情况就是 $p=1, k=n-m$. 要证明 $W^{m,1} \to L^{1}(H)$. 用方块覆盖, 每个方块的前m维数用局部估计, 余下的维数积分恰好是k维的积分, 这样就可以得到结果.

剩余的就是嵌入到Holder空间的情况. 它的证明用到的技巧是Morrey不等式. 注意这时需要区域满足强lipschitz条件, 如区域是两个拼起来的方形, 中间不连接, 那么是不能嵌入这样的空间的.

同样的, 指标也可以通过量纲计算. 比如 $mp > n >(m-1)p$, 那么有

$\alpha$ 就是对应的Holder空间的指数. 当 $p>1$, $n=(m-1)p$ 时, $\alpha = 1$, 则恰好不能嵌入到Lipschitz空间中. $p=1$ 时是可以的.

到目前为止, 有几个重要的不能进行嵌入的边界情况

前两个反例用单项式即可, 后两个用双对数函数.

还有一个有趣的例子, 即用半范数控制范数, 即

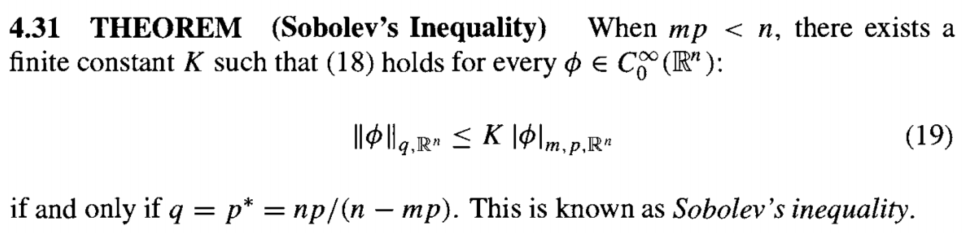
它只在临界情形成立. 因为回忆其它情形都是用到了插值.

插值定理

这里的插值定理是, 是否能用最高阶半范数和Lp范数来控制中间阶的半范数. 具体的定理如下:

证明思路来自于从1维出发, 然后高维用方向导数推广, 最后用归纳法推广到任意阶导数.

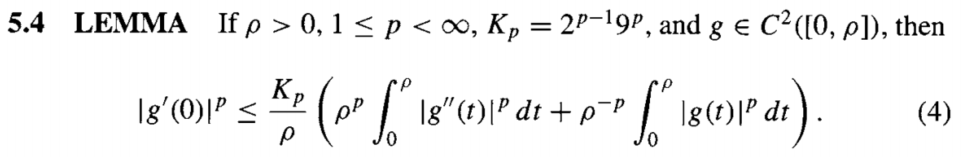
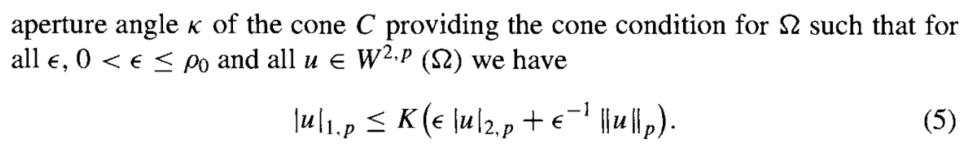
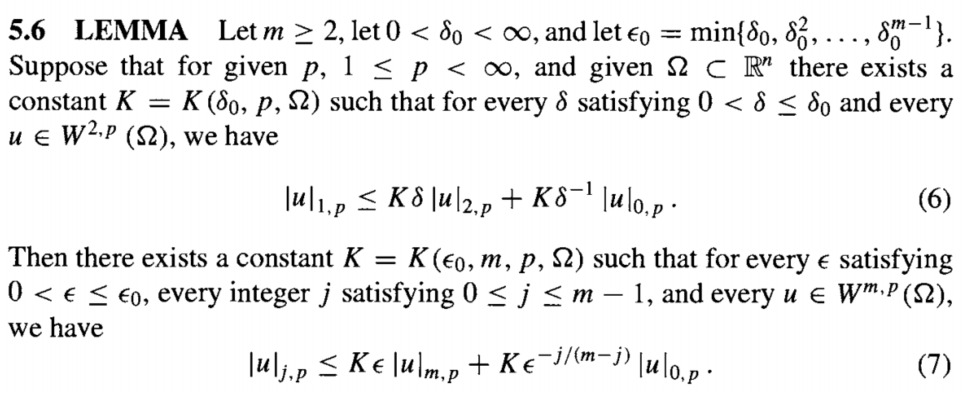
最后一个结果使用了Young不等式, 然后再用前面的插值.

紧嵌入

这里只放2个反例

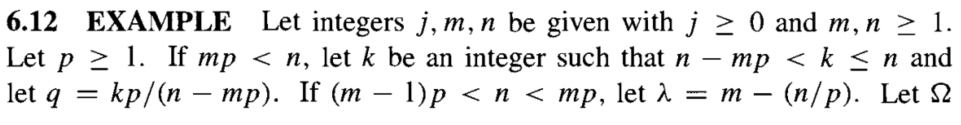
这两个反例本质上是说, 找一列不相交的开球和紧支撑在上面的光滑函数, 然后将函数进行平移和放缩.

比如临界情形

对应的嵌入都不是紧的. 取一列不相交的开球 $B_i$ 对应的光滑函数 $\varphi_i = r_i^{m-\frac{n}{p}}\varphi(\frac{x-a_i}{r_i})$, 则 $\varphi_i$ 在 $W^{m,p}$ 中有界. 但是在 $L^{p^*}(H)$ 中它们的范数都是常数, 所以不可能有收敛的子列.

本质上紧嵌入和普通嵌入的定理几乎没有区别, 只是各个嵌入的区间变成了开区间.

$L^p$ 空间的 pre-compact set

由Ascoli-Arzela 定理, 我们知道 $C(\overline{\Omega})$ 中的预紧集可以通过一致有界和等度连续来刻画. 那么在 $L^p$ 空间中, 有类似的结论.

$L^p(\Omega)$ 中的集合 $F$ 是预紧集的充分必要条件是

• $F$ 在 $L^p$ 中有界
• 对于 $\forall \epsilon > 0, \exists \delta > 0$ and 一个紧子集 $K \subset \Omega$, 使得对于 $\forall f \in F$, 有

  • $\int_{\Omega \setminus K}

    f

    ^p < \epsilon^p$

  • $|\tau_h \tilde f - \tilde f|_{L^p(K)} < \epsilon$, 当 $|h| < \delta$ 时成立. 这里 $\tilde f$ 是 $f$ 的零延拓, $\tau_h \tilde f(x) = \tilde f(x+h)$.

可以猜测到证明思路就是用 mollifier 进行逼近, 然后利用Ascoli-Arzela 定理.

充分性部分, 由于$C_c^\infty(\Omega)$ 在 $L^p(\Omega)$ 中稠密, 因此有对应的$\frac{\epsilon}{3}$ 网. 它们的supp的并就是对应的紧子集 $K$. 平移连续性直接用对应的逼近和这个网中函数的平移连续性来控制.

必要性部分, 不妨取$\Omega$是$R^n$. $\tilde K$ 是 $K$ 中函数的零延拓. 如果$\tilde K$ 在 $L^p(R^n)$ 中有网, 那么把这个网限制到$\Omega$上就是 $K$ 的网. 用 mollifier 进行逼近, 然后在G上利用Ascoli-Arzela 定理, 再把这个网零延拓回去就是 $\tilde K$ 的网.

紧嵌入

如果函数可导, 那么它的平移连续性是自动满足的. 因此它总是可以紧嵌入到低阶的Sobolev空间中. 再符合普通的连续嵌入, 得到全部的紧嵌入情形.

逼近

逼近是说, 如果用光滑函数逼近$W^{1,p}$中的函数, 那么它不可能有很好的更高阶导数的控制. 具体的定理如下:

证明思路是对积分余项的泰勒展开, 然后用磨光子进行卷积逼近.