HIF

Published:

学一下层次插值分解(Hierarchical Interpolative Factorization, HIF).

2D 串行

2分树数据结构

Hypoctree在下面将会被称为T

T的数据结构为

struct T {

    // 网格点结构
    using v2d = Eigen::Vector2d<double>;

    int* nodes; // 节点指针数组
    int num_nodes; // 节点数量

    // 每个节点的子节点列表
    // children[i] 存储第 i 个节点的所有子节点索引
    std::vector<std::vector<int>> children;


    // 每个节点的父节点索引
    std::vector<int> parent;

    // 每个level的节点范围
    // [lvlptr[i], lvlptr[i+1]) 表示第 i+1 层的节点索引范围
    std::vector<int> lvlptr;

    // 每个节点中的网格点坐标
    // xis[i] 存储第 i 个节点中的所有网格点坐标
    // 只有叶子节点才有实际的坐标数据
    std::vector<std::vector<v2d>> xis;

    // 每个节点对应的区域中心
    // centers[i] 存储第 i 个节点对应区域的中心坐标
    std::vector<v2d> centers;

    // 每个level中区域的半径
    // lsize[i] 存储第 i 层中区域的半径
    std::vector<double> lsize;

    // 每个节点的邻居节点列表
    // neighbors[i] 存储第 i 个节点的所有邻居节点索引
    std::vector<std::vector<int>> neighbors;
}

除了上述数据结构, 还需要下一个层次中的EdgeTree, 用于dim1消元

struct EdgeTree {
    std::vector<int> lvlptr; // 每个level的边范围, 其实是假的, 本质上只存了这一层的边
    std::vector<v2d> centers; // 每条边的中心位置
    std::vector<std::vector<v2d>> xis; // 每条边上的网格点坐标
    std::vector<std::vector<int>> neighbors; // 每条边的邻居边列表
    std::vector<std::vector<int>> parents; // 每条边的父边列表


};

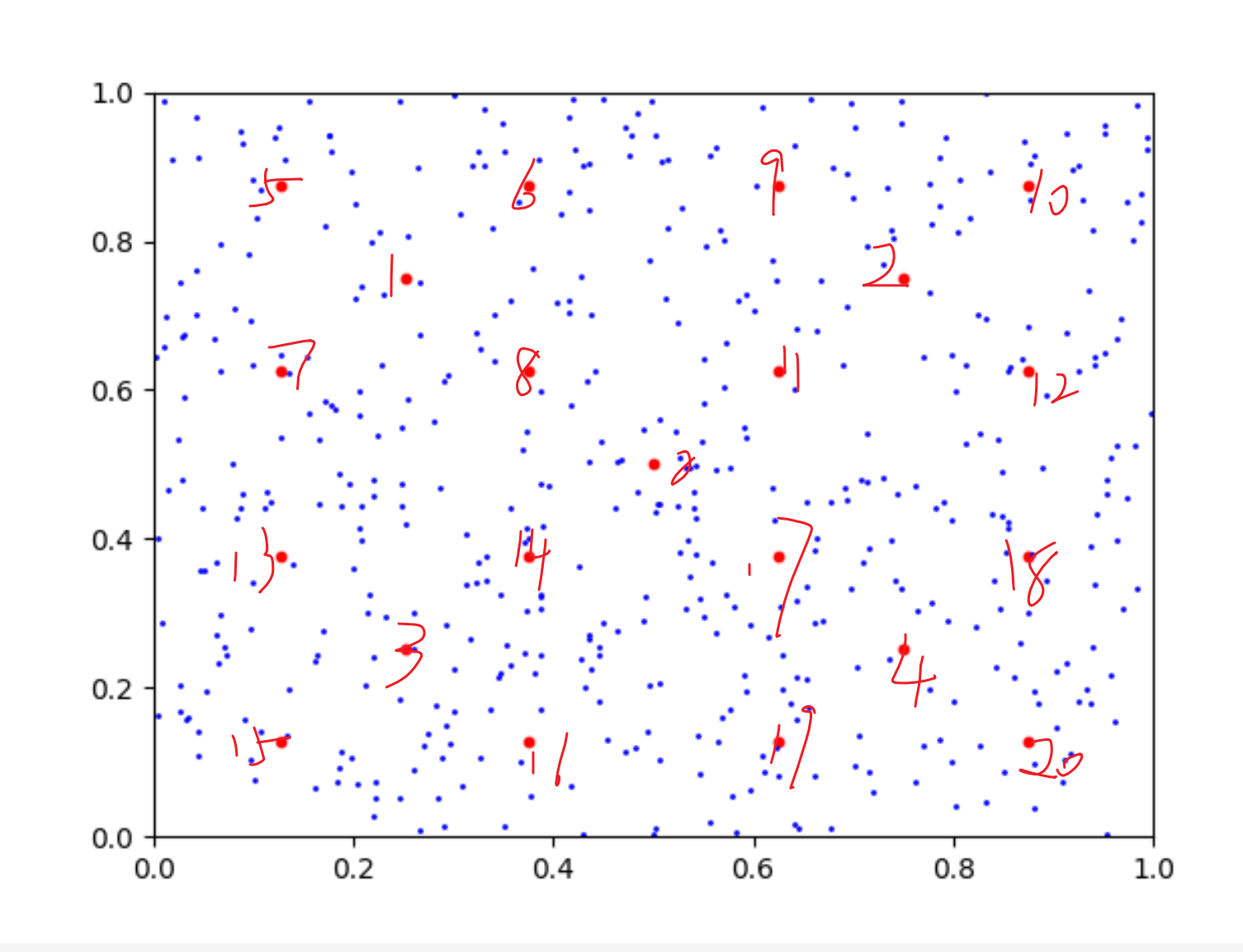
2D 四叉树

2D 下树的构建过程

这里只介绍EdgeTree的构建过程, Hypoctree的比较简单

  1. 从Hypoctree的当前层开始, 生成所有可能的边心相对于区域中心的位置偏移

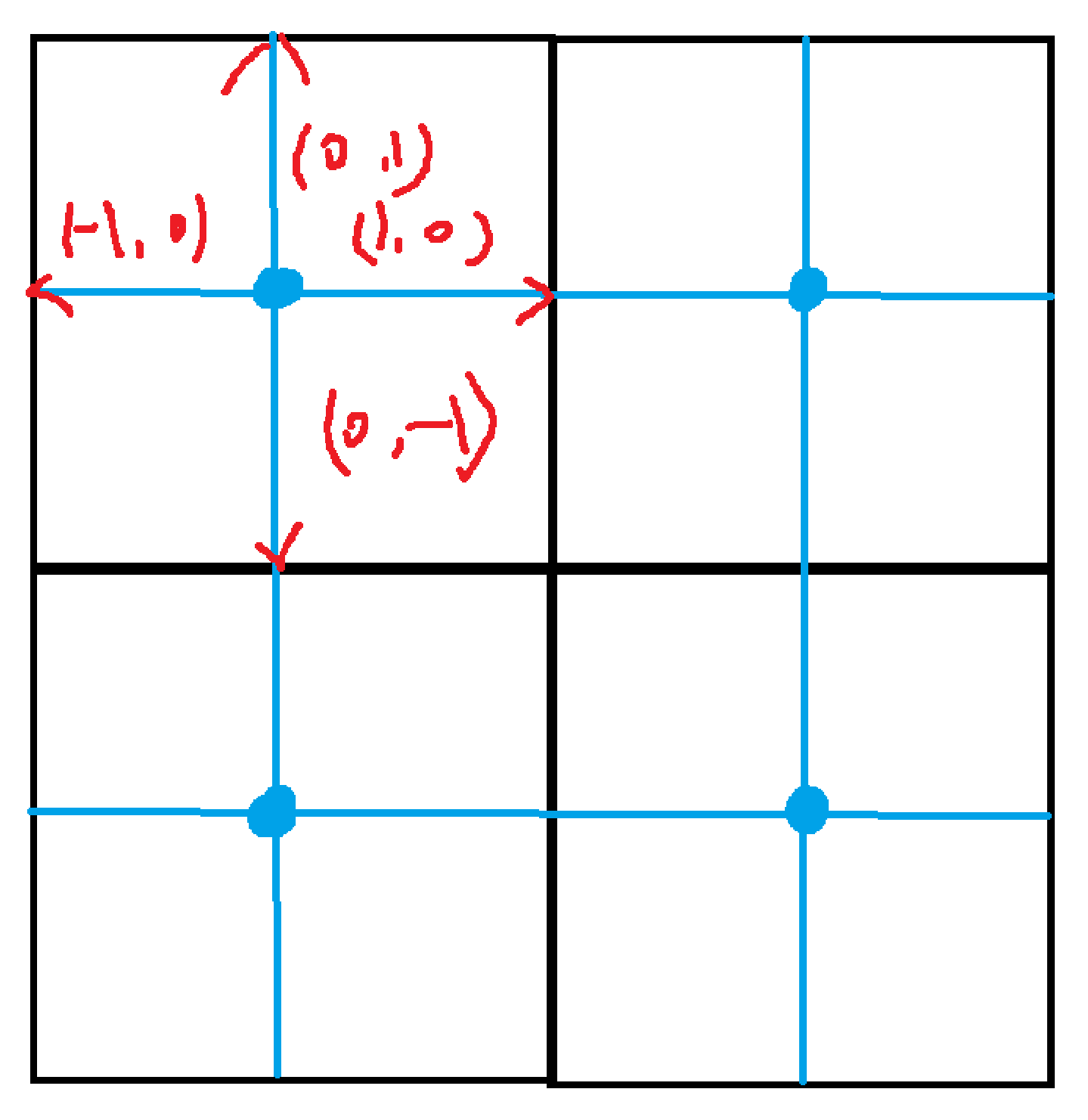
2D offset

  1. 获取所有的可能边心位置, 只保留被多个区域共享的边心, 丢掉边界上的孤立边心
  2. 将每个区域中的点加入最近的有效边心, 并在边心对应的节点中记录每个点的原来属于的区域. 记录每个边心的邻居, 用于计算插值分解.
  3. 如果是非均匀网格, 记录粗粒度叶子节点(通常用不上)

HIF 算法流程

需要存储的数据


struct HIF2D {
    T tree; // 四叉树数据结构

    using HIFFactor2DNode = struct {
        // 骨架点索引
        std::vector<int> sk;

        // 冗余点索引
        std::vector<int> rd;

        // 插值矩阵 T
        SparseMatrix<double> T;

        // LU 分解结果
        SparseMatrix<double> L;
        SparseMatrix<double> U;
        std::vector<int> P; // 置换矩阵, 存储行交换信息

        // E 和 F 矩阵
        SparseMatrix<double> E;
        SparseMatrix<double> F;
    };

    // 原始矩阵, 稀疏格式存储, csr
    SparseMatrix<double> A;

    // 所有的更新
    SparseMatrix<double> M;

    // IJV 列表
    std::vector<int> IJV_I;
    std::vector<int> IJV_J;
    std::vector<double> IJV_V;

    // 每个节点的HIF分解结果
    std::vector<HIFFactor2DNode> factors;
    // 每个level的节点范围
    // [factor_node_lvlptr[i], factor_node_lvlptr[i+1])
    // 表示第 i+1 层的节点索引范围
    std::vector<int> factor_node_lvlptr;

    // 未消去的节点列表
    // remains[i] = 0 表示第 i 个节点已被消去
    std::vector<int> remains;
};

最外层循环 — 对于每一个level进行处理

  1. 从子level收集所有的未消去网格点

  2. 删除子节点的所有网格点

  3. 对于当前层的每个节点进行dim2消元
  4. 对于当前层的每个节点进行dim1消元

内层循环 — 对于每一个节点进行处理

expand of 3: dim2 elimination

  1. 对该节点负责的所有网格点进行插值分解, 得到骨架点sk和冗余点rd以及插值矩阵T. 将树的remains对应的rd点标记为已消去.
  2. 将矩阵A与M在当前节点上对应的子矩阵进行相加得到真实的目前的子矩阵A_node. 对A_node用对应的插值矩阵T进行消元更新, 得到更新后的子矩阵A_node_new.

以下是矩阵的变化过程：

初始矩阵： \(\begin{bmatrix} A(\text{rd}, \text{rd}) & A(\text{rd}, \text{sk}) & A(\text{rd}, \text{oth}) \\ A(\text{sk}, \text{rd}) & A(\text{sk}, \text{sk}) & A(\text{sk}, \text{oth}) \\ A(\text{oth}, \text{rd}) & A(\text{oth}, \text{sk}) & A(\text{oth}, \text{oth}) \end{bmatrix}\)

经过消元后变为： \(\begin{bmatrix} A_{\text{new}}(\text{rd}, \text{rd}) & 0 & 0 \\ 0 & A_{\text{new}}(\text{sk}, \text{sk}) & A(\text{sk}, \text{oth}) \\ 0 & A(\text{oth}, \text{sk}) & A(\text{oth}, \text{oth}) \end{bmatrix}\)

  1. 将更新后的子矩阵A_node_new进行LU分解, 得到 P, L, U 三个矩阵. 并计算对应的E和F矩阵. 同时保存[rd],
  2. 计算(sk, sk)上的舒尔补 X = -E * F, 并将X更新到IJV列表中.

    每次回传的舒尔补都是针对当前节点的sk点的, 因为rd点已经被消去掉了.

  3. 将当前level的所有节点的更新都应用到M矩阵上. 具体操作为: 找到M的所有非零元, 将其更新到IJV列表中. 然后清空M矩阵.从IJV列表中重新构建M矩阵.

dim1 elimination 并没有和dim2有什么区别, 只是树是边构成的. 这个由边构成的树只有一层. 在做完消去之后要把边层中的骨架点重新加入回原来的dim2层次, 用于下一层的dim2消去

至此就是串行HIF2D的全流程, 唯一没有提及的就是插值分解是如何利用邻居选择代理曲面的, 不过这大概是纯粹的数学理论, 也就不作阐述.

可以看到它确实是可以并行的, 即每个节点可以抽象为单一的任务, 但是要在同一个level内如何分配worker给面单元和边单元以及处理单元内点的归属是需要一次通信的.

HIF 的并行化思路

树的分布式存储与并行构造

首先树的数据结构没有显著的变化, 每个进程存储所有的非网格点数据, 只分布存储网格点数据.

比较有趣的是确认每个块的方式是level+offset, level是每个维度2分的次数, offset是每个维度的偏移量, 比如 AreaBlock {level: [2, 3], offset: [3, 6]} refers to the area: x0 in $[\frac{3}{2^2}, \frac{4}{2^2})$, x1 in $[\frac{6}{2^3}, \frac{7}{2^3})$.

对于多个进程, 由于进程管理方式是确定性的, 所以每个进程可以直接计算出自己负责的块. 这一计算是在树构建前完成的. 对于DHIF, 进程数按照约定为$2^p$个, 也就是总是假设它可以随着维度被二分而被分到不同的区域上. 最终在p次二分后, 每个进程根据自己的global rank就可以计算出自己负责的区域块.

接着开始构建树.

在最开始, 所有进程同时构建根节点, 调用Cblacs_gridmap分配$1\times 2^p$的进程网格. rank 映射是平凡的.

为了接着构建子节点, 这里定义一个函数, 用来添加一个node到该进程的树中.

template <Int D>
void Tree<D>::appendNode(
    dvecnd center, Bound<D> b,
    Int parent,
    std::optional<Indices> child,
    std::optional<Indices> neighbor,
    NodeContext ctx,
    PIdx leader_proc,
    PIdx local_size
    );

它需要该节点的center, boundary, parent index, child indices, neighbor indices, 节点上下文(叶子节点/非叶子节点/边节点), 该节点的leader进程(负责该节点数据的进程), 以及该节点在leader进程上的本地大小(网格点数量).

这里NodeContext里存储的是负责该节点的进程组, 以及该进程组对应的BLACS上下文. 这里的BLACS上下文是为了后续调用ScaLAPACK的分布式矩阵运算做准备的.

构建树接下来就是开始对根节点进行划分. 对nlvl自增1. 然后开始循环直到nlvl达到预设的最大level.

首先找到所有需要划分的维度, 比如对于均匀的方形网格, 每个维度都需要划分. 每个进程维护一个lsize数组, 用来存储每个维度上当前节点的大小. 接着所有进程判断自己负责的上一个level中的节点是否有需要划分的维度(区域内点数大于最大叶子节点容量). 如果有, 那么就进行划分. 接着为了保证划分的一致性, 所有进程进行一次MPI_Allreduce操作, 确保所有进程的划分是一致的.

如果需要划分, 那么更新lsize, 对于每个需要划分的维度. 对于上一层的每个节点, 如果

  • finer case: 此时一个进程会负责多个子节点, 如果该节点与该进程负责的区域块有交集
  • corsar case: 此时多个进程会负责同一个子节点, 如果该节点和上一层该进程所持有的节点有交集 那么该进程都会调用splitNode和函数进行划分.

所以有趣的事情是要么一个进程负责多个子节点, 要么多个进程负责同一个子节点, 但是不会同时出现这两种情况. 另一件需要注意的事情是尽管进程可能会对多个节点进行划分(因为重合实际上包含了相邻的节点), 但是实际上所持有的节点仍然只有1个(粗粒度情形下).

在splitNode函数中:

首先计算该节点的子节点的数量, 获取全局通讯器. 然后获取该节点的leader进程rank以及该节点的进程组大小.

接下来计算本节点的所有子节点对应的区域块, 子节点的center, boundary等信息. 将所有子节点添加到当前节点的children列表中. 当前进程判断该被划分节点是否属于自己. 是否属于自己是通过ctxs_[curr].owing判断的. 要注意的是ctxs是每个进程不同的. 如果当前进程拥有该节点且判断拥有该子节点(该进程加入了对应子节点的管理进程组), 那么就从全局通信器中为该子节点创建通信器, 否则就创建空的通信器. 然后将该子节点添加到树中. 在ctxs_中记录该子节点的上下文信息. 如果拥有该子节点, 那么就在该进程的my_nodes中记录该子节点的索引.

由此可见只要进程拥有某个节点, 那么他就拥有该节点的通讯器, 尽管它不是leader进程.

由此递归地划分直到达到最大level.

可以注意到的一点是每个进程只持有整个树的一个局部, 也就是该进程拥有的节点以及该进程负责划分的所有节点的子节点.

另一个必须小心的地方在于每个进程看到的相同节点在进程内的编号是不同的

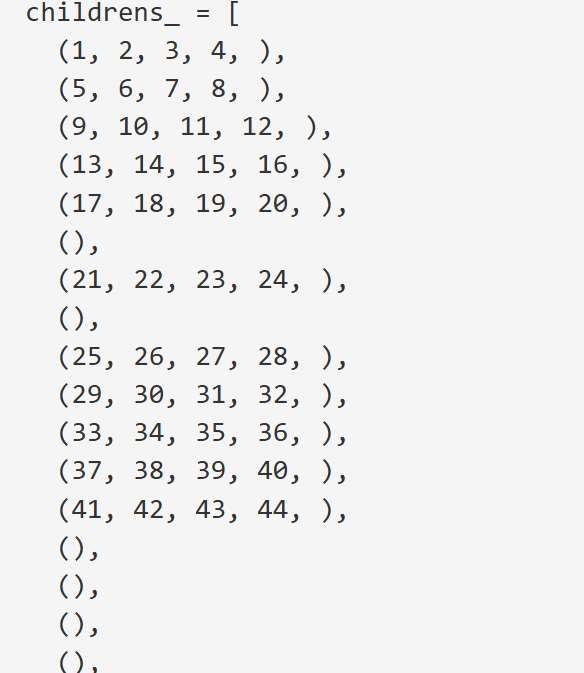p0 0号进程看到的树结构 p4 4号进程看到的树结构