Diffusion models.
Published:
今年学过不少有趣的扩散模型, 所以想写点东西记录一下.
Flow Matching
为了建模一个未知的分布 $q(x)$, flow matching 的想法是从一个简单的分布 $p(z)$ 通过神经网络映射到 $q(x)$. 但是直接学习映射的难度很大, 就像GAN一样, 非常难以训练. 因此FM的做法是连续的把 $p(z)$ 变成 $q(x)$.
\[X_t = \phi(X_0, t).\]最简单的做法是线性插值:
\[X_t = t X_1 + (1-t) X_0.\]$X_0$ 服从高斯分布. 直接写出速度场:
\[\frac{d}{dt} X_{t} = u(X_{t}, t) = X_1 - X_0 = X_1 - \frac{X_{t} - t X_1}{1-t} = \frac{X_1 - X_{t}}{1-t}.\]那么训练的目标就是让神经网络 $u_\theta(X_t, t)$ 去拟合上面的速度场:
\[L(\theta) = E_{t, X_0, X_1} [||u_\theta(X_t, t) - \frac{X_1 - X_{t}}{1-t}||^2] = E_{t, X_0, X_1} [||u_\theta(X_t, t) - (X_1 - X_0)||^2].\]学到的速度场就可以用来做采样了. 采样$x_0$ 后, 求解下面的ODE:
\[\frac{d}{dt} x(t) = u_\theta(x(t), t), \quad x(0) = x_0.\]试了在mnist上训了一个小模型, 以下是效果

DLM
和一个做扩散模型的朋友聊天感觉即和传统扩散模型不同, 也和当前decoder only 架构不同, 所以写点东西记录一下.
连续版本
连续版的DLM和图像扩散模型非常类似, 只是把图像的像素点换成了词向量. 在latent space中做连续扩散.
离散版本
离散版本是比较有趣的. 它直接在token level上做扩散, 不需要向连续空间的嵌入.
具体做法是定义一个absorbing process, 也就是随着时间的推移, token会越来越倾向于变成一个特殊的[mask] token. 这样在t=0的时候是原始token, t=T的时候是全是[mask] token.
然后训练一个transformer模型, 让它学会在任意时间点t, 给定一个部分mask的序列, 预测原始的token. 训练目标是最大化在所有时间点t上, 模型预测的mask掉的token的概率和原始token的概率的交叉熵.
下面是一个对比示意图, 来自于论文A Survey on Diffusion Language Models
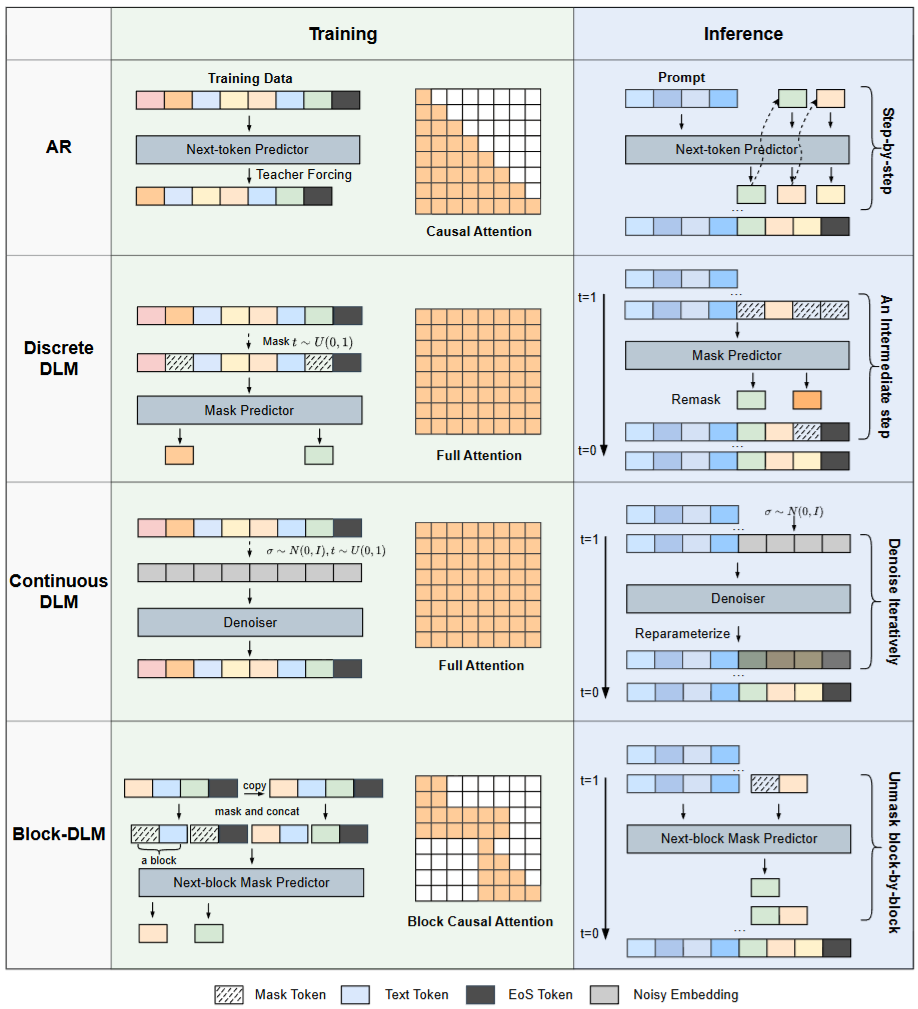
虽然看上去可以同时对多个token进行去噪, 但实际上推理的时候每次只按顺序生成一个token, 其他位置的token都作为条件输入给模型. 这样就和传统的自回归模型类似了. 据说是这样生成质量最好…
这样同样面临和自回归模型一样的问题, 就是长序列的o(n^2)复杂度, 如果模型采用了transformer架构的话. 并且由于没有自回归的限制, 每次unmask的token位置不同, 对kvcache的管理也会比较麻烦. 通常的做法就是局部稀疏attention, 或者每次unmask多个token, 在生成质量和效率上做trade-off.
不管怎么样, DLM是带有并行生成能力的, 和传统自回归的outline+refine的并行生成思路还是不太一样的.
自回归+扩散
对token进行分块, 每次扩散和去噪一个块, 块内用扩散, 块间用自回归.